How small are the fundamental particles of the Universe?

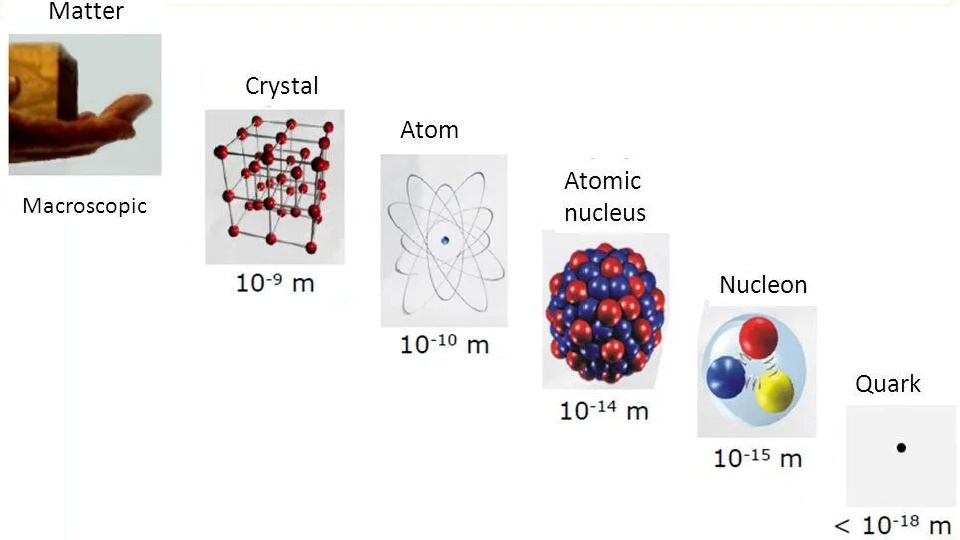
Imagine that you wanted to know what the matter around you was made of, at a fundamental level. How would you go about figuring out the answer? You might think to approach the problem by taking a piece of that matter and splitting it into small chunks, and then taking one of those chunks and further splitting it into tinier pieces, and so on and so on, until you could split it no longer. When you reached your limit, and found a component that was no longer splittable into anything smaller, that would serve as the best approximation of “fundamental” you could arrive at. Once you discover a component of matter that’s no longer divisible into smaller components, that’s a reasonable way to define fundamental.

For most of the 19th century, we thought that atoms were the fundamental constituents of matter; the Greek word that our work atom derives from, ἄτομος, literally means “uncuttable.” Today, we know that atoms themselves aren’t truly indivisible, but can be split into nuclei and electrons, and that while we cannot split the electron, nuclei can be broken up into protons and neutrons, which can be further subdivided into quarks and gluons. But are quarks, gluons, and electrons, among other particles that we consider to be fundamental today, truly uncuttable?

Many of us wonder if they might someday be split further, and how small their true size truly is. Are the particles of the Standard Model truly point-like? Here’s what we know so far.

A pentacene molecule, as imaged by IBM with atomic force microscopy and single-atom resolution. This was the first single-atom image ever taken, which took advantage of a new technique called in situ functionalization of the tip of the force probe.

The picture that you see, above, is truly remarkable: it’s an image of individual atoms, arranged into a particular molecular configuration, taken with a technique that’s not so different from an old-style photograph. The way photographs work is that light of a particular wavelength (or set of wavelengths) strikes an object, where some of those light waves travel through, unimpeded, while others are absorbed and still others are reflected. By either measuring the light that travels through the object or the light reflected off of the object, you can construct an image — either a negative or positive image, respectively — of your object.

What enables this property of matter: its ability to be photographed? It’s only permissible because of one particular, and often-counterintuitive, property of light: the fact that light behaves as a wave. All waves have a wavelength, or a characteristic length scale to them. If you’re attempting to image a very small object, you typically need to use light whose wavelength is smaller than the object in question, otherwise the wave will simply propagate past the object unimpeded. However, if the opposite is true, and the object you’re trying to image is physically larger than the wavelength of the light wave you’re using to probe the object, you’re going to be able to acquire an image of that object.

The size, wavelength, and temperature/energy scales that correspond to various parts of the electromagnetic spectrum. You have to go to higher energies, and shorter wavelengths, to probe the smallest scales. Ultraviolet light is sufficient to ionize atoms, but as the Universe expands, light gets systematically shifted to lower temperatures and longer wavelengths.

This gives us a tremendous amount of control over how we choose to look at a particular object: we need to choose an imaging wavelength that will give us high-quality resolution of the object that we want, but that won’t be of such a short wavelength (and, correspondingly, of such a high energy) that the act of striking the object with that wave causes damage or destruction. After all, the amount of energy something has increases at shorter and shorter wavelengths, and high-energy impacts can do things like ionize electrons, break atomic or molecular bonds, or even split an atom’s nucleus apart.

So what wavelength of light should you choose when it comes to probing the structure of matter? It would depend on the size of the system you’re observing, and what level of detail (or resolution) you need to obtain. These properties help explain why:

• we need relatively large antennae to pick up radio waves, because broadcast radio is at a long wavelength and you need a comparably sized antenna to interact with that signal,
• why you have holes in the door of your microwave oven, so that the long-wavelength microwave light gets reflected and stays inside, but the short-wavelength visible light can come out, allowing you to see what’s in there,
• and why the tiny dust grains in space are great at blocking short-wavelength (blue) light, are less good at longer-wavelength (red) light, and are absolutely lousy at blocking even longer-wavelength (infrared) light.

This animation shows the Bok globule Barnard 68 in a variety of visible and infrared wavelengths. As the longer wavelengths reveal, this is not a hole in the Universe but simply a dusty cloud of gas, where the longer (redder) wavelengths of light penetrate and pass through the dust. As dust clouds form and dissipate, the dust density can be revealed by examining the light blocked and transmitted by fixed, background objects.

So how would we go about obtaining images of matter, all the way down to the smallest possible scales? It would make sense to use photons, or quanta of light, as those are the tools we most commonly and successfully use to take images in the macroscopic world. it would be easy to assume that light, or photons, are really the way to go when it comes to imaging objects on all scales. After all, if you want to construct an image of something, why wouldn’t you use light for all of your purposes?

The thing is this: you could use light, but you aren’t required to. Physics, at its core, doesn’t care whether you’re a photon or not when it comes to constructing an image. All physics cares about is that you have a wave nature to you, and if you do, what your wavelength is. If you’re a quantum of light, that’s going to be your photon wavelength. But if you’re a different quantum particle, even one with a rest mass, like an electron, you’re still going to have a wavelength that’s related to your energy: your de Broglie wavelength.

In reality, whether you choose to use a light wave or a matter wave is irrelevant. All that matters is the wavelength. That’s how we can probe matter and determine the size of an object, down to any arbitrary scale we choose.

Freestanding paper made of carbon nanotubes, a.k.a. buckypaper, will prevent the passage of particles 50 nanometers and larger. It has unique physical, chemical, electrical, and mechanical properties. Although it can be folded or cut with scissors, it’s incredibly strong. With perfect purity, it’s estimated it could reach up to 500 times the strength of a comparable volume of steel. This image shows NanoLab’s buckypaper under a scanning electron microscope.

That’s right: matter, just like light, is fundamentally a wave as well as a particle, and quantum mechanics doesn’t just predict this, but observations and measurements bear this out. This property of matter was such a surprise when it was first revealed that scientists studied it ad nauseam, baffled and shocked at what they saw.

If you fired an electron through a slit in a barrier, it would show up in a small pile on the other side. If you cut a second slit very close to the first one, though, you wouldn’t get two piles, as you would have expected if electrons behaved as conventional, macroscopic particles of matter. Instead, you’d observe an interference pattern on the other side of the double slit. It was as though your electrons were truly behaving as waves, the same way that light waves, water waves, or any other known “wave” was seen to behave.

Things got even weirder when people tried to control the electrons, firing them one-at-a-time toward these two slits. They set up experiments to record where the electrons landed, one-at-a-time, on a screen behind the slit. As you fired more electrons, one after the other, that same interference pattern began to emerge. Not only did electrons behave as waves, but they didn’t require other electrons in order to create interference; each single electron behaved as though it could interfere with itself.

The wave pattern for electrons passing through a double slit, one-at-a-time, with both slits open/available to the electron. If you measure “which slit” the electron goes through, you destroy the quantum interference pattern shown here. However, the wave-like behavior remains so long as the electrons have a de Broglie wavelength that’s smaller than the size of the slit they’re passing through. This wave-like and particle-like behavior has been demonstrated for electrons, photons, and even larger, composite entities.

So if electrons have a wavelength, just like photons do, how can you potentially use them (or any form of matter) to probe these tiny, fundamental scales? You simply do what you’d do for photons: go to higher energies, which correspond to smaller wavelengths and shorter distance scales.

The higher-energy you can impart to your particle, the smaller the size of a structure you can probe. If you can crank up the energy on your electrons (or photons, or protons, or your particle of choice), the shorter your wavelength will be, and the better the resolution of the image you ultimately construct will be as well. If you can measure exactly which conditions are needed to split your non-fundamental (i.e., composite) particle apart, you can determine the needed energy threshold, which teaches you about the physical size of the (composite) particle in question.

This technique enabled us to determine that:

• Atoms aren’t indivisible, but are made of electrons and nuclei with a combined size of ~1 Å, or ~10^-10 meters.
• Atomic nuclei can be split apart into protons and neutrons, each with a size of ~1 fm, or ~10^-15 meters.
• And if you bombard electrons or quarks or gluons with high-energy particles, they show no evidence of internal structure at all, down to a size of ~10^-19 meters.

The sizes of composite and elementary particles, with possibly smaller ones lying inside what’s known. With the advent of the LHC, we now can restrict the minimum size of quarks and electrons to 10^-19 meters, but we don’t know how far down they truly go, and whether they’re point-like, finite in size, or actually composite particles.

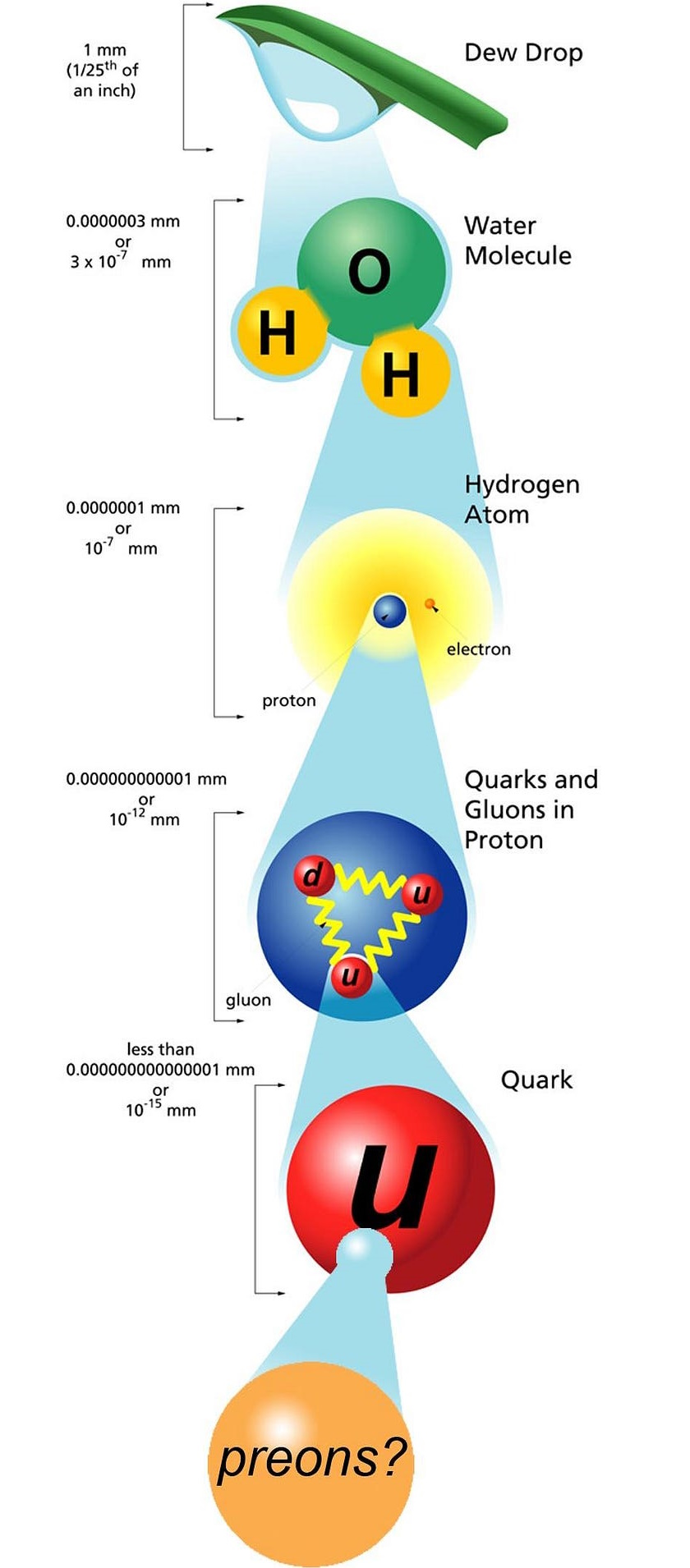
Today, our experiments show no evidence for compositeness to any of the Standard Model particles down to the absolute limits of what we’ve been able to probe. Based on experiments conducted at high-energy particle colliders, we can conclude that each of the Standard Model particles is truly fundamental, at least as far as we’ve been able to measure: down to this scale of ~10^-19 meters.

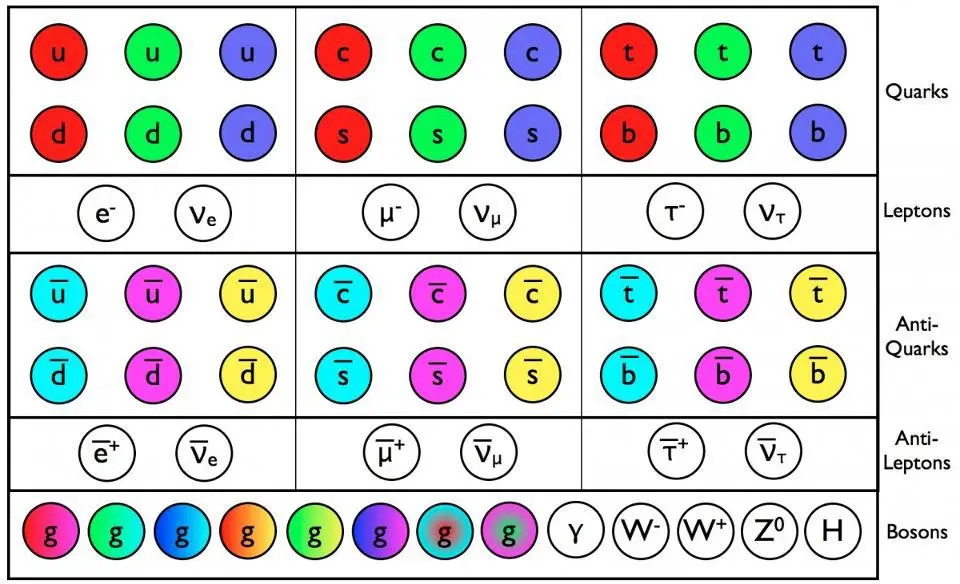
Fundamental, we believe, should mean that the particle is absolutely indivisible: it cannot be broken apart into smaller entities that make it up. In simpler terms, we should not be able to crack it open and see what’s inside in any sort of physical sense. According to our best theory of particle physics, the Standard Model, all of the known particles:

• the six types of quarks and six antiquarks,
• the three charged leptons and three antileptons,
• the three neutrinos and antineutrinos,
• the eight gluons,
• the photon,
• the W-and-Z bosons,
• and the Higgs boson,

are expected to be indivisible and fundamental and point-like. Experiments, to the limits that we’ve been able to perform them, are entirely consistent with this notion.

The particles and antiparticles of the Standard Model have now all been directly detected, with the last holdout, the Higgs Boson, falling at the LHC earlier this decade. All of these particles can be created at LHC energies, and the masses of the particles lead to fundamental constants that are absolutely necessary to describe them fully. These particles can be well-described by the physics of the quantum field theories underlying the Standard Model, but they do not describe everything, like dark matter.

But here’s the thing: we don’t know whether this “indivisible” property of Standard Model particles is deeply true down to the smallest possible physical scales or not. Sure, the Standard Model says that this is the way that things are, but we know that the Standard Model doesn’t give us the final answer to every question or inquiry we have about the Universe. In fact, we know that at some level, the Standard Model must break down and be wrong, because it doesn’t account for a whole host of things we can measure about our cosmos. In particular, the Standard Model cannot explain:

• gravity,
• dark matter,
• dark energy,
• or the preponderance of matter (and not antimatter) in the Universe.

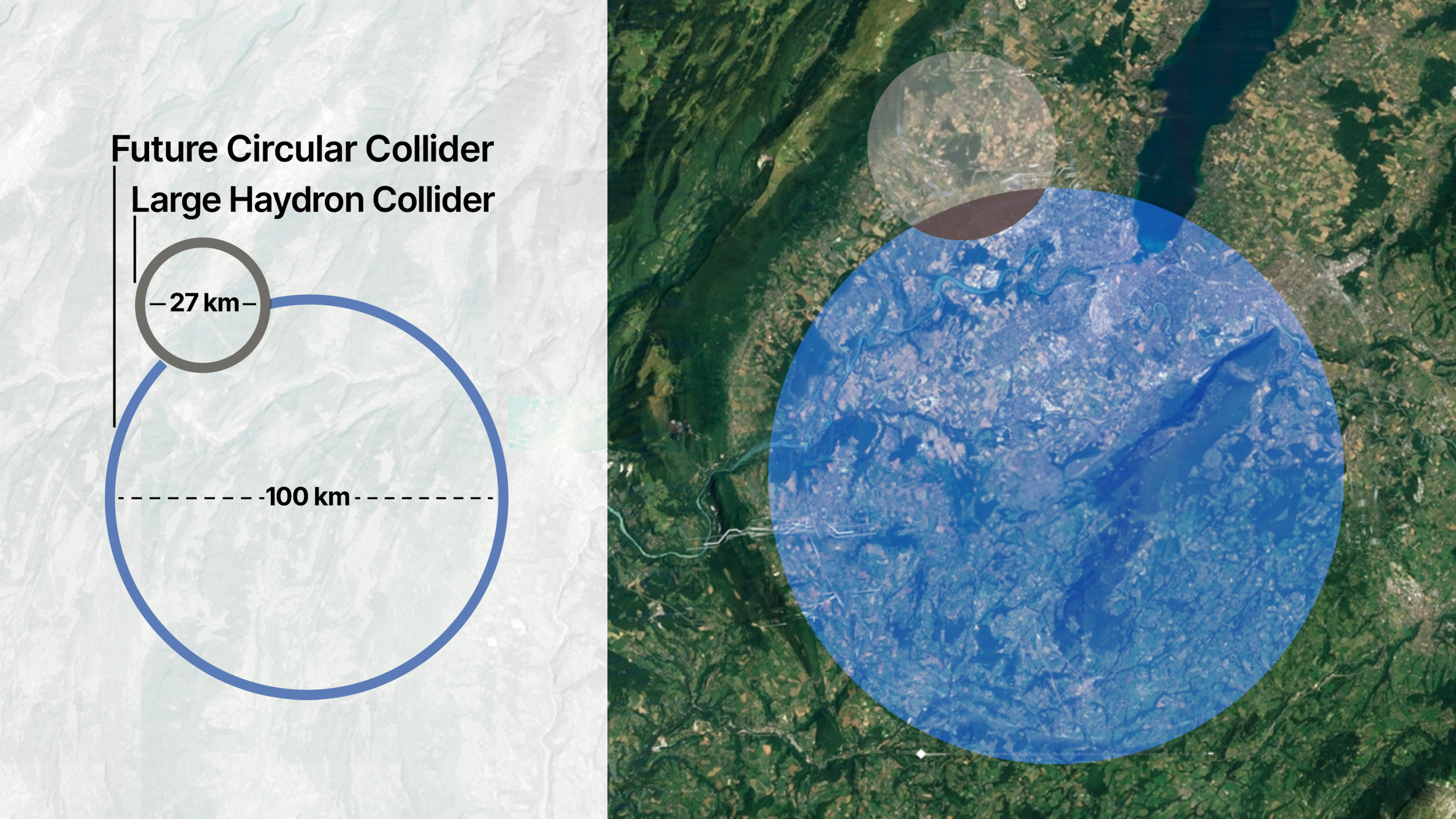
There has to be something out there that goes beyond the properties of nature that we’ve already uncovered. Sure, it’s always possible that there are new particles out there that are outside of the Standard Model, and they hold the key to solving those mysteries. But it’s also possible that the known particles that we think are fundamental, point-like, and indivisible today actually aren’t. Perhaps, if we go to high-enough energies and small-enough wavelengths, we’ll be able to see that at some point, somewhere between the LHC’s maximum energy scales and the (factor of a quadrillion greater) Planck energy scale, there’s actually more to the Universe than we presently know.

The objects we’ve interacted with in the Universe range from very large, cosmic scales down to about 10^-19 meters, with the newest record set by the LHC. There’s a long, long way down (in size) and up (in energy) to the scales that the hot Big Bang achieves, which is only about a factor of ~1000 lower than the Planck energy. If the Standard Model particles are composite in nature, higher energy probes may reveal that, but ‘fundamental’ must be the consensus position today.

When it comes to the fundamental particles of nature, this technique of smashing particles into one another is the most sensitive tool we have at our disposal to investigate them and their properties. We can observe the results of these collisions, including:

• what particles are created and/or destroyed,
• whether there’s evidence for “hard sphere” scattering and, if so, what the sizes and cross-sections of those spheres are,
• whether there’s any “missing energy” or “missing momentum,” which would indicate invisible (and potentially new) particles,

along with all sorts of other reconstructible properties concerning the debris from the collision, including a census of “daughter particles” that they produce. The fact that none of these fundamental particles have ever been observed to crack apart, show an interior structure, or give us a hint that they have a finite size to them is the best evidence we have, to date, concerning their fundamental, indivisible nature.

But the curious among us won’t simply be satisfied with the present limits that we’ve set. If we had stopped at atoms, we never would have discovered the quantum secrets that lie within the atom. If we had stopped with protons and neutrons, we never would have discovered the underlying structure of the normal matter that fills the Universe. And if we stop where we are right now, with the Standard Model, who knows what sorts of secrets we’ll never uncover?

The Future Circular Collider (in blue) would overlap slightly with the current Large Hadron Collider, but requires an additional ring (and tunnel) somewhere upward of 80 km in circumference: dwarfing the LHC’s current 27 km circumference. Bigger tunnels and stronger magnets are needed for a more energetic hadron collider, with the FCC proposing ~16 T magnets, approximately double the LHC’s current magnet strength.

Science is not some half-baked, assume-the-conclusion enterprise, where we know the answers going into an experiment and only perform it to confirm what we know. Science is about discovery. It’s about pushing past the frontiers of what’s already known, and learning about nature by asking it physical questions about itself. It’s about looking where we’ve never looked before, and finding out what lies behind that veil of uncertainty. The day may come where all of humanity takes a look at what we know and the magnitude of what we’d have to build to take that next step and say, “There’s no way we can do that,” but that’s not where we are today.

We know what’s possible, and we have the technological know-how to make it happen. We know how to go to the next level. We know how to go to the next order-of-magnitude and the next significant digit in collider energy, and that means we can probe nature more sensitively, at smaller scales and sizes. The Standard Model particles show no signs of compositeness at the Large Hadron Collider, from cosmic rays, or from any other experiment, but those are just the current limitations of what’s presently known. Is the Universe we understand today truly all there is out there? It can’t be. Until we’ve discovered the last of nature’s secrets about what’s truly fundamental, we cannot allow ourselves to stop the search.

This article was originally published in August of 2019. It was updated in February of 2025.